by ゲスト » 2025/2/06(木) 21:03:40
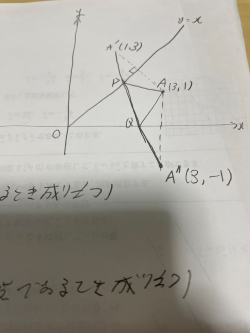
直線$y=x$に関してAと対称な点をA'とする。
また、$x$軸に関してAと対称な点をA"とする。
このとき
$AP=A'P $
また
$ AQ=A^{"}Q$
△APQの周の長さは
$AP+PQ+QA =A'P+PQ+QA^{"} \geq$
4点A',P,Q,A"が一直線上にあるとき最小となる。
直線A'A"は2点(1,3),(3,-1)を通るから直線A'A"の式を$y=ax+b$とおくと
\[3=a+b,-1=3a+b \]
よって,$a=-2,b=5$
Pは$x=-2x+5$より $x=\frac{5}{3}$
Qは$0=-2x+5$より$x=\frac{5}{2}$
よって、答えは
\[P(\frac{5}{3},\frac{5}{3}) Q(\frac{5}{2},0) \]
- 添付ファイル
-
- 2025_0206_B.png (92.22 KiB) 閲覧された回数 4459 回
直線$y=x$に関してAと対称な点をA'とする。
また、$x$軸に関してAと対称な点をA"とする。
このとき
$AP=A'P $
また
$ AQ=A^{"}Q$
△APQの周の長さは
$AP+PQ+QA =A'P+PQ+QA^{"} \geq$
4点A',P,Q,A"が一直線上にあるとき最小となる。
直線A'A"は2点(1,3),(3,-1)を通るから直線A'A"の式を$y=ax+b$とおくと
\[3=a+b,-1=3a+b \]
よって,$a=-2,b=5$
Pは$x=-2x+5$より $x=\frac{5}{3}$
Qは$0=-2x+5$より$x=\frac{5}{2}$
よって、答えは
\[P(\frac{5}{3},\frac{5}{3}) Q(\frac{5}{2},0) \]